Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Решение других типов уравнений с использованием линейных уравнений - СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ - ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ
Цель: познакомить учащихся с другими типами уравнений.
Планируемые результаты: получить представление об уравнениях, сводящихся к линейным.
Тип урока: урок-исследование.
Ход урока
I. Сообщение темы и цели урока
II. Работа по теме урока
План урока
1. Нелинейные уравнения.
2. Уравнения с модулем.
3. Уравнения с параметрами.
Рассмотрим другие типы уравнений, которые могут быть решены с использованием линейных уравнений.
1. Нелинейные уравнения
Пример 1
Уравнение х(х - 1) = 0 на основании распределительного свойства может быть записано в виде х2 - х = 0 и является квадратным, так как содержит член х2.
Квадратные уравнения вы будете изучать только в следующем классе. Однако данное уравнение легко решается. Его левая часть представляет собой произведение двух множителей. Это произведение равно нулю, если один из множителей равен нулю. Получаем х = 0 или х - 1 = 0 (откуда х = 1). Следовательно, данное уравнение имеет два корня: х = 0 и х = 1.
Пример 2
Уравнение (3х - 7)(х2 + 1)(2х + 3) = 0 является уравнением четвертой степени. Для его решения можно использовать тот же подход, что и в предыдущей задаче. Произведение трех множителей равно нулю, если один из них равен нулю. Получаем линейное уравнение 3x - 7 = 0 (его корень ![]() ), квадратное уравнение х2 + 1 = 0 (которое, очевидно, корней не имеет) и линейное уравнение 2х + 3 = 0 (его корень
), квадратное уравнение х2 + 1 = 0 (которое, очевидно, корней не имеет) и линейное уравнение 2х + 3 = 0 (его корень ![]() ). Итак, данное уравнение имеет два корня:
). Итак, данное уравнение имеет два корня: ![]() и х = -1,5.
и х = -1,5.
2. Уравнения с модулем
Прежде всего, напомним определение модуля. Модулем числа (выражения) а называется само это число (выражение) а, если оно неотрицательное, и число (выражение) -а, если число (выражение) а отрицательное. Модуль числа (выражения) обозначается символом |a|. Определение модуля можно записать короче:
![]()
Величина |а| имеет простой геометрический смысл — расстояние от тонки а на координатной оси до начала отсчета (точки 0).
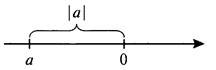
В задачах также часто встречается величина |а - b|. Ее геометрический смысл — расстояние между точками а и b на координатной оси.

Напомним основные свойства модулей, часто используемые при решении задач:
1. |а| ≥ 0, т. е. модуль любого числа (выражения) — неотрицательное число (выражение). При этом |а| = 0 только при а = 0.
2. |а| = |-а|, т. е. модули противоположных чисел (выражений) равны.
3. |a|2 = а2, т. е. квадрат модуля числа (выражения) равен квадрату самого числа (выражения).
4. |а ∙ b| = |а| ∙ |b|, т. е. модуль произведения двух чисел (выражений) равен произведению модулей этих чисел (выражений).
5. ![]() т. е. модуль частного двух чисел (выражений) равен частному модулей этих чисел (выражений). При этом очевидно, что b ≠ 0.
т. е. модуль частного двух чисел (выражений) равен частному модулей этих чисел (выражений). При этом очевидно, что b ≠ 0.
Теперь рассмотрим уравнения с модулем.
Пример 3
Решим уравнение |2х - 5| = 0.
Очевидно, что в соответствии со свойством 1 это равенство выполняется только в том случае, когда подмодульное выражение 2x - 5 само равно нулю. Получаем линейное уравнение 2x - 5 = 0 или 2x = 5, откуда ![]() — единственный корень данного уравнения.
— единственный корень данного уравнения.
Пример 4
Решим уравнение |3х + 8| = 1.
Так как |1| = 1, то данное уравнение можно записать в виде |3x + 8| = |1|. Поскольку модули двух величин равны, то сами величины или равны, или противоположны по знаку (свойство 2).
Получаем два линейных уравнения:
а) 3х + 8 = 1 или 3х = -7, его корень ![]()
б) 3х + 8 = -1 или 3х = -9, его корень х = -3.
Итак, данное уравнение имеет два корня: ![]() и х = -3.
и х = -3.
Пример 5
Решим уравнение |5х + 1| = |3х - 9|.
Вновь используем свойство 2: если модули двух величин равны, то сами величины или равны, или противоположны по знаку. Получаем два линейных уравнения:
а) 5х + 1 = 3х - 9, или 5х - 3х = -1 - 9, или 2х = -10, его корень х = -5;
б) 5x + 1 = -(3х - 9), или 5х + 1 = -3х + 9, или 5х + 3х = -1 + 9, или 8х = 8, его корень х = 1.
Итак, данное уравнение имеет два корня: х = -5 и х = 1.
Пример 6
Решим уравнение |3х + 4| = х.
Так как модуль некоторого выражения равен величине х, то в соответствии со свойством 1 эта величина х ≥ 0. Для таких значений х подмодульное выражение 3х + 4 > 0. Тогда по определению модуля |3х + 4| = 3х + 4. Данное уравнение имеет вид 3х + 4 = х, или 3х - х = -4, или 2х = -4, откуда х = -2. Однако это значение не удовлетворяет условию х ≥ 0 и не является корнем данного уравнения.
Итак, данное уравнение корней не имеет.
Пример 7
Решим уравнение |5х| = 5х.
На основании свойства 4 имеем |5х| = |5| ∙ |х| = 5 ∙ |х|. Тогда данное уравнение запишем в виде 5 ∙ |х| = 5 ∙ х. Разделим обе части уравнения на число 5 и получим более простое уравнение |х| = х. Так как модуль некоторого выражения равен величине х, то в соответствии со свойством 1 эта величина х ≥ 0. Для таких значений х подмодульное выражение х > 0. Тогда по определению модуля |х| = х. Данное уравнение имеет вид х = х. Очевидно, это равенство выполняется при всех значениях х. Но эти значения х должны удовлетворять условию х ≥ 0. Поэтому все такие х являются решениями уравнения.
Итак, все неотрицательные числа будут решениями данного уравнения.
Более сложные уравнения с модулем пока рассматриваться не будут.
3. Уравнения с параметрами
В некоторые уравнения, помимо неизвестного х, входит еще одна переменная (параметр), которая может принимать произвольные значения. Как правило, в этих уравнениях требуется найти решение для любого значения параметра или исследовать решение уравнения (при этом иногда само решение находить не надо).
Пример 8
Найдем значение параметра о, при котором уравнение (3а + 1) ∙ х = 2а + 6 имеет корень х = 2.
Так как данное уравнение имеет корень х = 2, то при подстановке этого значения в уравнение получим верное равенство (3а + 1) ∙ 2 = 2а + 6. Это равенство является линейным уравнением для нахождения нужного значения а. Получаем, раскрывая скобки и решая линейное уравнение: 6а + 2 = 2а + 6, или 6а - 2а = 6 - 2, или 4а = 4, откуда а = 1. Итак, при а = 1 данное уравнение имеет корень х = 2.
Это легко проверить. При подстановке значения а = 1 в данное уравнение оно имеет вид (3 ∙ 1 + 1) ∙ х = 2 ∙ 1 + 6 или 4х = 8. Действительно, корень этого уравнения х = 2.
Пример 9
При каком значении параметра а уравнение (2а - 4) ∙ х + а - 1 = 4а - 7 имеет три различных корня?
Прежде всего, запишем это линейное уравнение в стандартном виде. Для этого перенесем слагаемые, не зависящие от х, в правую часть уравнения и приведем подобные члены: (2а - 4) ∙ х = 4а – а - 6 или (2а - 4) ∙ х = 3а - 6. Известно, что линейное уравнение с ∙ х = b имеет более одного корня (бесконечно много корней) только при условии с = 0 и b = 0, т. е. 2а - 4 = 0 и 3а - 6 = 0. Эти линейные уравнения имеют один и тот же корень а = 2.
Итак, при а = 2 данное уравнение (2а - 4) ∙ х + а - 1 = 4а - 7 имеет бесконечно много корней.
Поэтому три любых различных числа, например числа 5, -2, -7, будут корнями данного уравнения.
Пример 10
Решим уравнение а(а - 2) ∙ х = 5(а - 2) при всех значениях параметра а.
Это линейное уравнение уже записано в стандартном виде с ∙ х = b, где с = а(а - 2) и b = 5(a - 2).
Далее вспомним три возможных случая решения линейного уравнения.
1. Если с ≠ 0 (т. е. а(а - 2) ≠ 0 или а ≠ 0 и а ≠ 2), то уравнение имеет единственный корень ![]()
2. Если с = 0 при а = 0, то найдем значение b = 5(а - 2) = -10. Так как с = 0 и b ≠ 0, то в этом случае уравнение решений не имеет.
3. Если с = 0 при а = 2, то найдем значение b = 5(a - 2) = 5(2 - 2) = 5 ∙ 0 = 0. Так как с = 0 и b = 0, то в этом случае любое число х является корнем уравнения.
Итак, при а ≠ 0 и а ≠ 2 х = 5/a, при а = 0 решений нет, при а = 2 х — любое число.
Пример 11
При каких целых значениях параметра а корнем уравнения (а - 2) ∙ х = 3 является целое число?
Очевидно, что при а = 2 данное линейное уравнение решений не имеет. При а ≠ 2 уравнение имеет единственный корень ![]() . Так как по условию число а — целое, то и число а – 2 будет целым.
. Так как по условию число а — целое, то и число а – 2 будет целым.
Корень ![]() будет целым числом, если число а - 2 будет делителем числа 3. Число 3 имеет четыре делителя: ±1, ±3. Рассмотрим все возможные случаи: а – 2 = 1 (тогда а = 3), а - 2 = -1 (тогда а = 1), a - 2 = 3 (тогда а = 5), а - 2 = -3 (тогда а = -1). Итак, только при целых значениях а, равных 3, 1, 5, -1, данное уравнение имеет целые корни.
будет целым числом, если число а - 2 будет делителем числа 3. Число 3 имеет четыре делителя: ±1, ±3. Рассмотрим все возможные случаи: а – 2 = 1 (тогда а = 3), а - 2 = -1 (тогда а = 1), a - 2 = 3 (тогда а = 5), а - 2 = -3 (тогда а = -1). Итак, только при целых значениях а, равных 3, 1, 5, -1, данное уравнение имеет целые корни.
III. Задания на уроке и на дом
1. Решите уравнение:
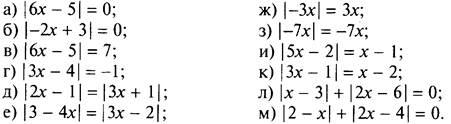
(Ответы:
а) 5/6;
б) 3/2;
в) -1/3 и 2;
г) корней нет;
д) -2 и 0;
е) 5/7 и 1;
ж) х ≥ 0;
з) х ≤ 0;
и) корней нет;
к) корней нет;
л) 3;
м) 2.)
2. Решите уравнение:
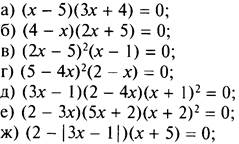
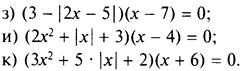
(Ответы:
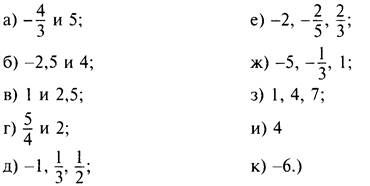
3. Решите уравнение при всех значениях параметра:
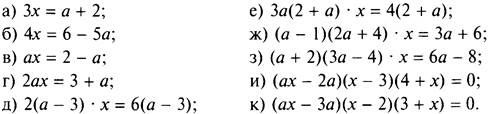
(Ответы:
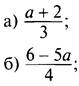
в) при ![]() при а = 0 решений нет;
при а = 0 решений нет;
г) при ![]() при а = 0 решений нет;
при а = 0 решений нет;
д) при а ≠ 3 х = 3, при а = 3 х — любое число;
е) при ![]() при а = -2 х — любое число;
при а = -2 х — любое число;
ж) при а ≠ -2 и ![]() при а = -2 x — любое число, при a = 1 решений нет;
при а = -2 x — любое число, при a = 1 решений нет;
з) при а ≠ -2 и ![]() при а = -2 решений нет, при a = 4/3 x — любое число;
при а = -2 решений нет, при a = 4/3 x — любое число;
и) при а ≠ 0 x1 = -4, х2 = 2, х3 = 3, при а = 0 х — любое число;
к) при а ≠ 0 х1 = -3, х2 = 2, х3 = 3, при а = 0 х — любое число.)
4. При каких значениях а число 3 является корнем уравнения?
![]()
(Ответы: а) -1/5; б) 8/5; в) при любых значениях а; г) таких значений а нет.)
5. При каких значениях а два уравнения имеют одинаковый корень?
а) 3х + 7 = 0 и 2х - 5а = 0;
б) 3х + 2 = 0 и ах - 5 = 0.
Найдите этот корень.
(Ответы: а) при ![]() б) при а = -7,5 х = -2/3.)
б) при а = -7,5 х = -2/3.)
6. При каких целых значениях а корнем уравнения будет целое число?
![]()
Найдите такие корни.
(Ответы:
а) при а = -1 х = -1, при а = 0 х = -3, при а = 2 х = 1, при а = 1 х = 3;
б) при а = -3 х = -1, при а = 0 х = 5, при а = -1 х = -5, при а = 2 х = 1;
в, г) таких значений а нет.)
7. При каких значениях параметра а уравнение:
а) (2а + 3) ∙ х - 2а = 3(а + 2) имеет единственный корень;
б) (2а + 3) ∙ х - 3а = 3(а + 3) имеет 11 различных корней;
в) (2а + 3) ∙ х - 3а = 3(а + 2) не имеет корней?
(Ответы: а) при а ≠ -1,5; б) при а = -1,5; в) при а = -1,5.)
8. Решите уравнение при всех значениях параметра а:

(Ответы:
а) при а ≠ 2 х = 2, при а = 2 решений нет;
б) при а ≠ -2 х = -a/2 при а = -2 решений нет;
в) при а ≠ 1,5 х = 3 - а, при а = 1,5 решений нет;
г) при а ≠ 2/3х = 4 - 3а, при а = 2/3 решений нет.)
IV. Подведение итогов урока